Digital Twins in Medicine, How Simulation Works, The Schlieren Method
📚 Free education is abundant, all over the Internet. It's the desire to learn that's scarce.
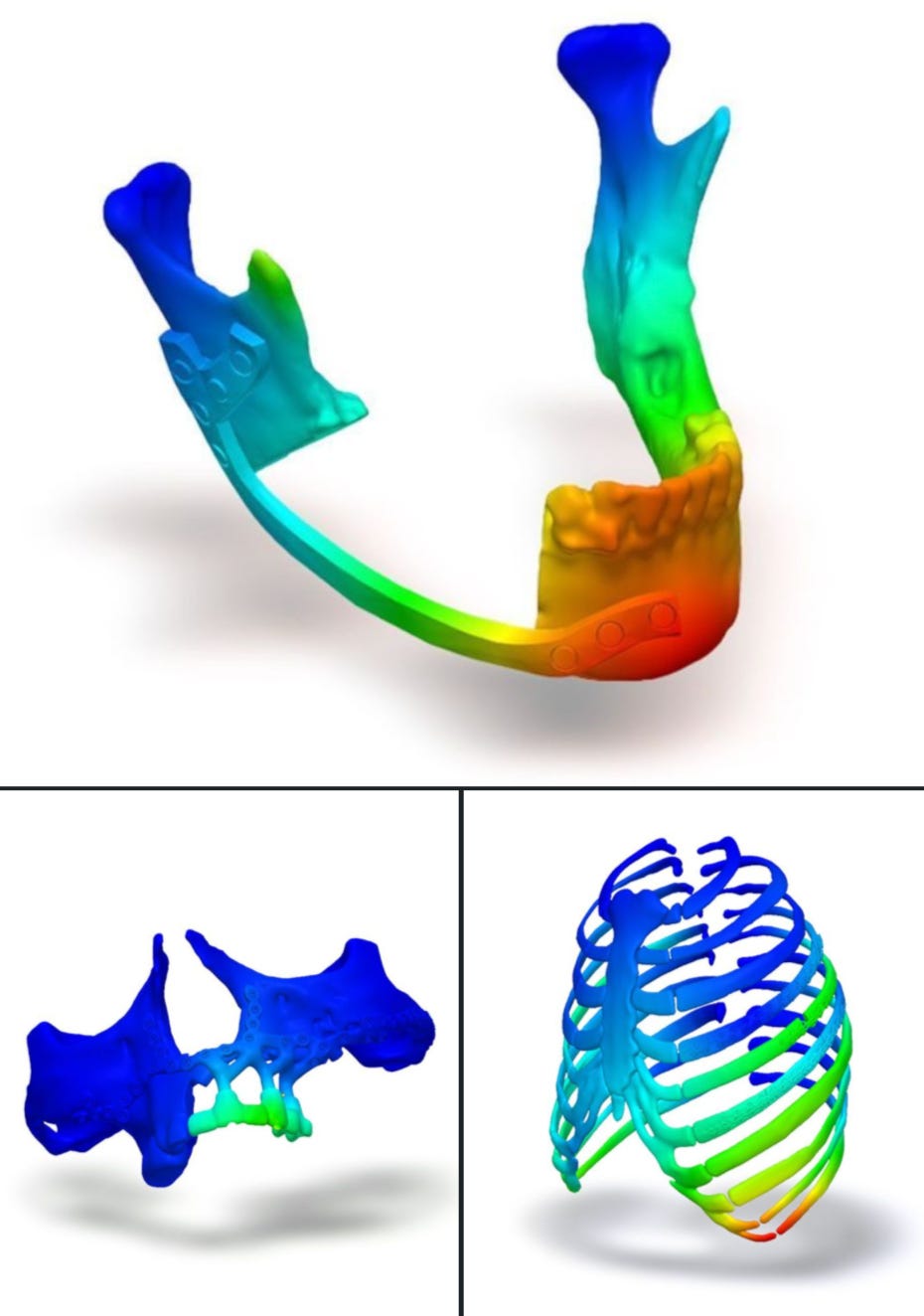
💻 Digital Twins in Medicine
💦 But How DO Fluid Simulations Work?
Fluid simulations. How on is it possible that a computer can recreate the crashing waves, the rolling clouds and the swirling smoke that we see in our daily lives, phenomena which seem characterized by randomness and chaos? This video will attempt to explain exactly how the mathematics behind fluid simulations work.
💦 The Navier-Stokes Equations
In 1845, Sir George Stokes had derived the equation of motion of a viscous flow by adding Newtonian viscous terms, thereby the Navier-Stokes Equations had been brought to their final form which has been used to generate numerical solutions for fluid flow ever since.
In this equation, the formula for mass continuity is missing and other assumptions go into this equation. You can find the full derivation of the equation here.
🦴 Finite Element Method for Medicine
In this numerical method, a complex shape is divided into many small, simple geometries, such as cuboids.
The finite element method easily calculates the simple geometries' physical behavior. The individual simple geometries‘ results are then combined to recreate the physical behavior of the entire body.
📚 Can Physics-Informed Neural Networks beat the Finite Element Method?
TL;DR: “Considering the solution time and accuracy, PINNs are not able to beat the finite element method in our study.”
The recent success of deep neural networks at various approximation tasks has motivated their use in the numerical solution of PDEs. These so-called physics-informed neural networks and their variants have shown to be able to successfully approximate a large range of partial differential equations. So far, physics-informed neural networks and the finite element method have mainly been studied in isolation of each other.
♨️ The Schlieren Method
Schlieren imaging systems have been used since the early 1800’s to visualize fluctuations in optical density. As a dynamic and straightforward visualization tool, these systems are primarily applied to conduct qualitative visual studies.
Schlieren optics provide an informative, non-intrusive method for studying transparent and optical media. It is beneficial to use them in fluid dynamics studies because they are sensitive to changes and do not interfere with flow. They are also used to study optical media and changes in refractive index within the material. Most commonly, schlieren systems have been applied to visualize diverse subjects such as striations in blown glass, inhalation in humans and animals, shock waves from a plane in flight, and heat emanating from a system. Source
💻 Engineering Tool of the Week – SU2
Computational analysis tools have revolutionized the way we design engineering systems, but most established codes are proprietary, unavailable, or prohibitively expensive for many users. The SU2 team is changing this, making multiphysics analysis and design optimization software freely available and involving everyone in its creation and development.
📚Book of the Week
A Voyage Through Turbulence
Turbulence is widely recognized as one of the outstanding problems of the physical sciences, but it still remains only partially understood despite having attracted the sustained efforts of many leading scientists for well over a century. This book will provide absorbing reading for every scientist, mathematician and engineer interested in the history and culture of turbulence, as background to the intense challenges that this universal phenomenon still presents.
Watch this series online: https://www.bilibili.com/video/av810855508/
❤️ Support the Blog & Newsletter
Let’s connect on Twitter or Instagram or LinkedIn!
For any business-related issues or collaborations, feel free to write me an email to support@jousefmurad.com!
Keep engineering your mind! 🧠
Jousef