./episode_162.sh

📚 Anyone who has never made a mistake has never tried anything new.

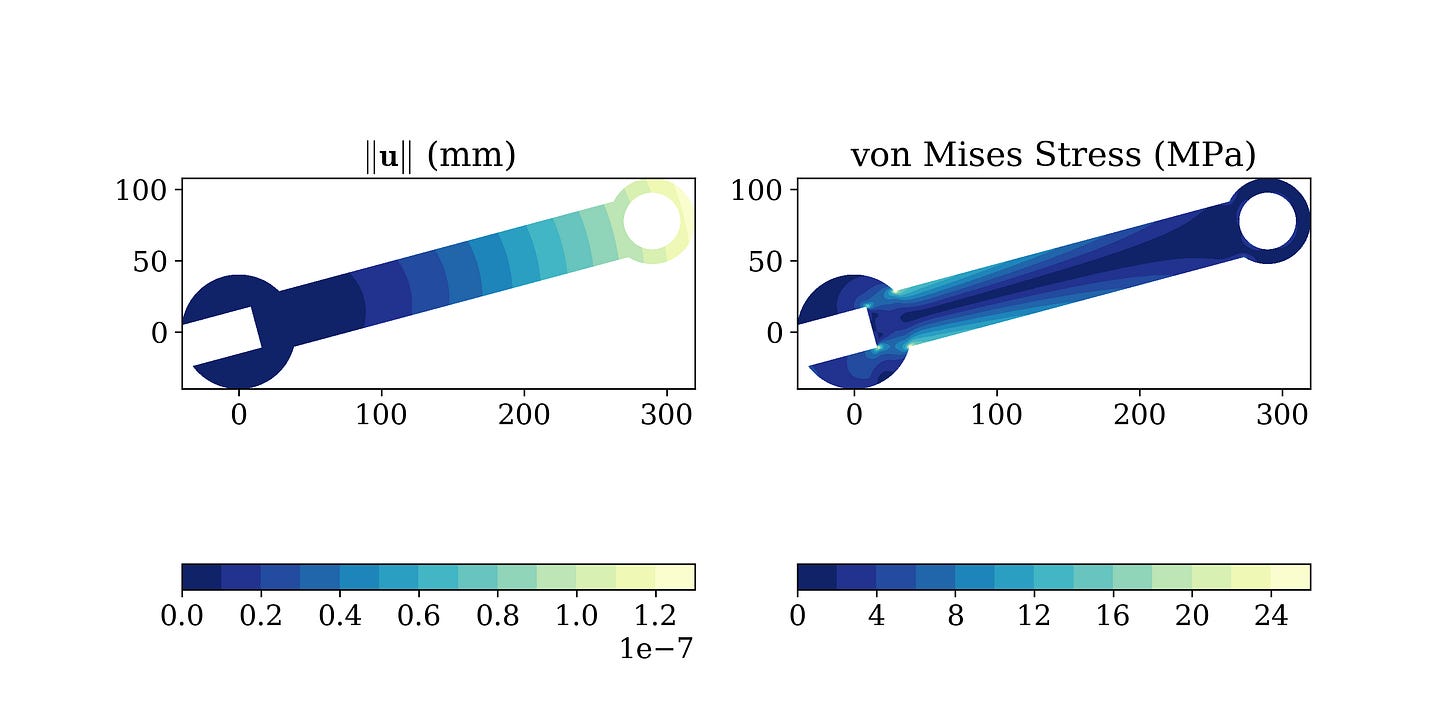
💡 Introduction to the Finite Element Method (Coding)

This repository contains teaching resources for an introductory course on Finite Element Analysis. The course emphasizes on the solution, through finite element algorithms, of the theory of elasticity boundary value problem. It combines theoretical aspects and computational implementations in Python.

💦 Φ-SO : Physical Symbolic Optimization - Learning Physics from Data

The Physical Symbolic Optimization package uses deep reinforcement learning to discover physical laws from data. Here is Φ-SO discovering the analytical expression of a damped harmonic oscillator.

🌎 Repo: https://github.com/WassimTenachi/PhySO

💦 High Quality Fluid Mechanics Video Collection

In 1961, Ascher Shapiro founded the National Committee for Fluid Mechanics Films (NCFMF) in cooperation with the Education Development Center and released a series of 39 videos and accompanying texts which revolutionized the teaching of fluid mechanics.

🌀 Turbulence: Finding Order in Chaos

It defines the shape of the cars we drive and the planes we fly on, yet it remains largely invisible. You can see it in the plume of a cigarette or your breath on a cold morning. Turbulence is all around of us but for many the word turbulence is largely associated with a bumpy flight. Neil will introduce you to the chaotic side of nature that remains one of physics greatest unsolved mysteries.

Dr. Neil Ashton discusses how our understanding of turbulence is enabling us to unravel some of the mysteries of nature. We learn how the flipper of a humpback whale inspired the look of one of the latest F1 cars, and why golf balls have dimples. By using some of the biggest supercomputers in the world, our knowledge of turbulence is bringing a new era of discovery.

🤓 Eighty Years of the Finite Element Method: Birth, Evolution, and Future

This document presents comprehensive historical accounts on the developments of fnite element methods (FEM) since 1941, with a specifc emphasis on developments related to solid mechanics. We present a historical overview beginning with the theoretical formulations and origins of the FEM, while discussing important developments that have enabled the FEM to become the numerical method of choice for so many problems rooted in solid mechanics.

 Physics-Constrained ML for Scientific Computing

A fundamental challenge is that the predictions of deep-learning models trained on physical data typically ignore fundamental physical principles. Such models might, for instance, violate system conservation laws: the solution to a heat transfer problem may fail to conserve energy, or the solution to a fluid flow problem may fail to conserve mass.

Similarly, a model’s solution may violate boundary conditions — say, allowing heat flow through an insulator at the boundary of a physical system. This can happen even when the model’s training data includes no such violations: at inference time, the model may simply extrapolate from patterns in the training data in an illicit way.

---

💻 Engineering Tool of the Week - FEniCSx

FEniCSx is a popular open-source computing platform for solving partial differential equations (PDEs). FEniCSx enables users to quickly translate scientific models into efficient finite element code. With the high-level Python and C++ interfaces to FEniCSx, it is easy to get started, but FEniCSx offers also powerful capabilities for more experienced programmers. FEniCSx runs on a multitude of platforms ranging from laptops to high-performance clusters.

---

📚Book of the Week

“I do like CFD”

"I do like CFD, VOL.1"  is a book on Computional Fluid Dynamics: the first one in a series to come. It is written by Dr. Katate Masatsuka, bringing those CFD know-how to the public.

---

🙃 Meme of the Week

---

• 🤝 Collaboration Requests

• ❤️ Support the Blog & Newsletter

---

Let’s connect on Twitter or Instagram or LinkedIn!

For any business-related issues or collaborations, feel free to email me at support@jousefmurad.com!

Keep engineering your mind! 🧠

Jousef